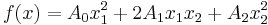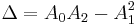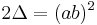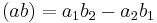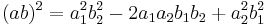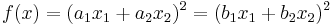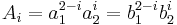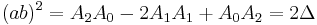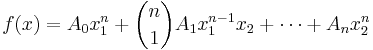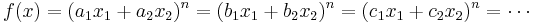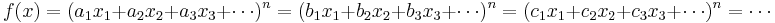Symbolic method
In mathematics, the symbolic method in invariant theory is an algorithm developed by Arthur Cayley, Siegfried Heinrich Aronhold (1858), Alfred Clebsch (1861), and Paul Gordan (1887) in the 19th century for computing invariants of algebraic forms. It is based on treating the form as if it were a power of a degree one form.
Contents |
Symbolic notation
The symbolic method uses a compact but rather confusing and mysterious notation for invariants, depending on the introduction of new symbols a, b, c, ... (from which the symbolic method gets its name) with apparently contradictory properties.
Example: the discriminant of a binary quadratic form
These symbols can be explained by the following example from (Gordan 1887, volume 2, pages 1-3). Suppose that
is a binary quadratic form with an invariant given by the discriminant
The symbolic representation of the discriminant is
where a and b are the symbols. The meaning of the expression (ab)2 is as follows. First of all, (ab) is a shorthand form for the determinant of a matrix whose rows are a1, a2 and b1, b2, so
Squaring this we get
Next we pretend that
so that
and we ignore the fact that this does not seem to make sense if f is not a power of a linear form. Substituting these values gives
Higher degrees
More generally if
is a binary form of higher degree, then one introduces new variables a1, a2, b1, b2, c1, c2, with the properties
What this means is that the following two vector spaces are naturally isomorphic:
- The vector space of homogeneous polynomials in A0,...An of degree m
- The vector space of polynomials in 2m variables a1, a2, b1, b2, c1, c2, ... that have degree n in each of the m pairs of variables (a1, a2), (b1, b2), (c1, c2), ... and are symmetric under permutations of the m symbols a, b, ....,
The isomorphism is given by mapping an−j
1aj
2, bn−j
1bj
2, .... to Aj. This mapping does not preserve products of polynomials.
More variables
The extension to a form f in more than two variables x1, x2,x3,... is similar: one introduces symbols a1, a2,a3 and so on with the properties
See also
References
- Aronhold, Siegfried Heinrich (1858), "Theorie der homogenen Functionen dritten Grades von drei Veränderlichen." (in German), Journal für die reine und angewandte Mathematik 55: 97–191, ISSN 0075-4102, http://resolver.sub.uni-goettingen.de/purl?GDZPPN00215028X
- Clebsch, A. (1861), "Ueber symbolische Darstellung algebraischer Formen" (in German), Journal für Reine und Angewandte Mathematik 59: 1–62, ISSN 0075-4102, http://resolver.sub.uni-goettingen.de/purl?PPN243919689_0059
- Dieudonné, Jean; Carrell, James B. (1970), "Invariant theory, old and new", Advances in Mathematics 4: 1–80, http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6W9F-4D7JKM7-1&_user=1495569&_coverDate=02%2F28%2F1970&_rdoc=1&_fmt=high&_orig=search&_origin=search&_sort=d&_docanchor=&view=c&_acct=C000053194&_version=1&_urlVersion=0&_userid=1495569&md5=66afdc20312efc67ffb295764befef82&searchtype=a, pages 32–37, "Invariants of n-ary forms: the symbolic method. Reprinted as Dieudonné, Jean; Carrell, James B. (1971), Invariant theory, old and new, Academic Press, ISBN 0122155408
- Dolgachev, Igor (2003), Lectures on invariant theory, London Mathematical Society Lecture Note Series, 296, Cambridge University Press, doi:10.1017/CBO9780511615436, ISBN 978-0-521-52548-0, MR2004511
- Gordan, Paul (1887), Kerschensteiner, Georg, ed., Vorlesungen über Invariantentheorie (2nd ed.), New York: Chelsea Publishing Co., ISBN 978-0-8284-0328-3, MR917266, http://books.google.com/books?isbn=978-0-8284-0328-3
- Grace, John Hilton; Young, Alfred (1903), The Algebra of invariants, Cambridge University Press
- Hilbert, David (1993) [1897], Theory of algebraic invariants, Cambridge University Press, ISBN 978-0-521-44457-6, MR1266168, http://books.google.com/books?isbn=0521449030
- Koh, Sebastian S., ed. (1987), Invariant Theory, Lecture Notes in Mathematics, 1278, ISBN 3540183604
- Kung, Joseph P. S.; Rota, Gian-Carlo (1984), "The invariant theory of binary forms", American Mathematical Society. Bulletin. New Series 10 (1): 27–85, doi:10.1090/S0273-0979-1984-15188-7, ISSN 0002-9904, MR722856, http://www.ams.org/journals/bull/1984-10-01/S0273-0979-1984-15188-7